Aplicas la estadística elemental
Población
En estadística, también llamada universo o colectivo, es el conjunto de elementos de referencia sobre el que se realizan unas de las observaciones. Población es el conjunto sobre el que estamos interesados en obtener conclusiones (hacer inferencia).una población es un conjunto de sujetos o individuos con determinadas características demográficas, de la que se obtiene la muestra o participantes en un estudio epidemiológico a la que se quiere extrapolar los resultados de dicho estudio (inferencia estadística). La estadística es comúnmente considerada como una colección de hechos numéricos expresados en términos de una relación sumisa, y que han sido recopilado a partir de otros datos numéricos.
Muestra
Es un subconjunto de casos o individuos de una población estadística.
Las muestras se obtienen con la intención de inferir propiedades de la totalidad de la población, para lo cual deben ser representativas de la misma. Para cumplir esta característica la inclusión de sujetos en la muestra debe seguir una técnica de muestreo. En tales casos, puede obtenerse una información similar a la de un estudio exhaustivo con mayor rapidez y menor coste.
Por otra parte, en ocasiones, el muestreo puede ser más exacto que el estudio de toda la población porque el manejo de un menor número de datos provoca también menos errores en su manipulación. En cualquier caso, el conjunto de individuos de la muestra son los sujetos realmente estudiados.
El número de sujetos que componen la muestra suele ser inferior que el de la población, pero suficiente para que la estimación de los parámetros determinados tenga un nivel de confianza adecuado. Para que el tamaño de la muestra sea idóneo es preciso recurrir a su cálculo.
Medidas de tendencia central: para datos agrupados y no agrupados
Al describir grupos de observaciones, con frecuencia es conveniente resumir la información con un solo número. Este número que, para tal fin, suele situarse hacia el centro de la distribución de datos se denomina medida o parámetro de tendencia central o de centralización. Cuando se hace referencia únicamente a la posición de estos parámetros dentro de la distribución, independientemente de que ésta esté más o menos centrada, se habla de estas medidas como medidas de posición.1 En este caso se incluyen también los cuantiles entre estas medidas.
Entre las medidas de tendencia central tenemos:
Moda.
La moda se refiere al dato más repetido, el valor de la variable con mayor frecuencia absoluta.
Su cálculo es extremadamente sencillo, pues sólo necesita un recuento. En variables continuas, expresadas en intervalos, existe el denominado intervalo modal o, en su defecto, si es necesario obtener un valor concreto de la variable, se recurre a la interpolación.
Por ejemplo, el número de personas en distintos vehículos en una carretera: 5-7-4-6-9-5-6-1-5-3-7. El número que más se repite es 5, entonces la moda es 5.
Hablaremos de una distribución bimodal de los datos, cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima. Cuando en una distribución de datos se encuentran tres o más modas, entonces es multimodal. Por último, si todas las variables tienen la misma frecuencia diremos que no hay moda.
Cuando tratamos con datos agrupados en intervalos, antes de calcular la moda, se ha de definir el intervalo modal. El intervalo modal es el de mayor frecuencia absoluta.
La moda, cuando los datos están agrupados, es un punto que divide el intervalo modal en dos partes de la forma p y c-p, siendo c la amplitud del intervalo, que verifiquen que:
Siendo 
la frecuencia absoluta del intervalo modal y 
y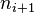 
las frecuencias absolutas de los intervalos anterior y posterior, respectivamente, al
la frecuencia absoluta del intervalo modal y y 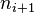las frecuencias absolutas de los intervalos anterior y posterior, respectivamente, al
Las calificaciones en la asignatura de Matemáticas de 39 alumnos de una clase viene dada por la siguiente tabla (debajo):
| Calificaciones | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Número de alumnos | 2 | 2 | 4 | 5 | 8 | 9 | 3 | 4 | 2 |
Hallar la moda de la distribución:
2, 3, 3, 4, 4, 4, 5, 5 Mo= 4
Si en un grupo hay dos o varias puntuaciones con la misma frecuencia y esa frecuencia es la máxima, la distribución esbimodal o multimodal, es decir, tiene varias modas.
1, 1, 1, 4, 4, 5, 5, 5, 7, 8, 9, 9, 9Mo= 1, 5, 9
Cuando todas las puntuaciones de un grupo tienen la misma frecuencia, no hay moda.
2, 2, 3, 3, 6, 6, 9, 9
Si dos puntuaciones adyacentes tienen la frecuencia máxima, la moda es el promedio de las dos puntuaciones adyacentes.
0, 1, 3, 3, 5, 5, 7, 8Mo = 4
Cálculo de la moda para datos agrupados
1º Todos los intervalos tienen la misma amplitud.
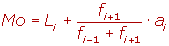
Li es el límite inferior de la clase modal.
fi es la frecuencia absoluta de la clase modal.
fi--1 es la frecuencia absoluta inmediatamente inferior a la en clase modal.
fi-+1 es la frecuencia absoluta inmediatamente posterior a la clase modal.
ai es la amplitud de la clase.
También se utiliza otra fórmula de la moda que da un valor aproximado de ésta:
Ejemplo
Calcular la moda de una distribución estadística que viene dada por la siguiente tabla:
| fi | |
|---|---|
| [60, 63) | 5 |
| [63, 66) | 18 |
| [66, 69) | 42 |
| [69, 72) | 27 |
| [72, 75) | 8 |
| 100 |
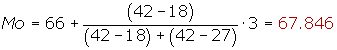
2º Los intervalos tienen amplitudes distintas.
En primer lugar tenemos que hallar las alturas.
La clase modal es la que tiene mayor altura.
La fórmula de la moda aproximada cuando existen distintas amplitudes es:
Ejemplo
En la siguiente tabla se muestra las calificaciones (suspenso, aprobado, notable y sobresaliente) obtenidas por un grupo de 50 alumnos. Calcular la moda.
| fi | hi | |
|---|---|---|
| [0, 5) | 15 | 3 |
| [5, 7) | 20 | 10 |
| [7, 9) | 12 | 6 |
| [9, 10) | 3 | 3 |
| 50 |
Mediana
Es el valor que ocupa el lugar central de todos los datos cuando éstos están ordenados de menor a mayor.
La mediana se representa por Me.
La mediana se puede hallar sólo para variables cuantitativas.
Cálculo de la mediana
1 Ordenamos los datos de menor a mayor.
2 Si la serie tiene un número impar de medidas la mediana es la puntuación central de la misma.
2, 3, 4, 4, 5, 5, 5, 6, 6Me= 5
3 Si la serie tiene un número par de puntuaciones la mediana es la media entre las dos puntuaciones centrales.
7, 8, 9, 10, 11, 12Me= 9.5
Cálculo de la mediana para datos agrupados
La mediana se encuentra en el intervalo donde la frecuencia acumulada llega hasta la mitad de la suma de las frecuencias absolutas.
Es decir tenemos que buscar el intervalo en el que se encuentre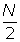 
.
.
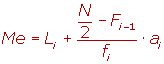
Li es el límite inferior de la clase donde se encuentra la mediana.
es la semisuma de las frecuencias absolutas.
Fi-1 es la frecuencia acumulada anterior a la clase mediana.
ai es la amplitud de la clase.
La mediana es independiente de las amplitudes de los intervalos.
Ejemplo
Calcular la mediana de una distribución estadística que viene dada por la siguiente tabla:
| fi | Fi | |
|---|---|---|
| [60, 63) | 5 | 5 |
| [63, 66) | 18 | 23 |
| [66, 69) | 42 | 65 |
| [69, 72) | 27 | 92 |
| [72, 75) | 8 | 100 |
| 100 |
100 / 2 = 50
Clase modal: [66, 69)
Media aritmética
La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos.
es el símbolo de la media aritmética.
Ejemplo
Los pesos de seis amigos son: 84, 91, 72, 68, 87 y 78 kg. Hallar el peso medio.
Media aritmética para datos agrupados
Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la media es:
Ejercicio de media aritmética
En un test realizado a un grupo de 42 personas se han obtenido las puntuaciones que muestra la tabla. Calcula la puntuación media.
| xi | fi | xi · fi | |
|---|---|---|---|
| [10, 20) | 15 | 1 | 15 |
| [20, 30) | 25 | 8 | 200 |
| [30,40) | 35 | 10 | 350 |
| [40, 50) | 45 | 9 | 405 |
| [50, 60 | 55 | 8 | 440 |
| [60,70) | 65 | 4 | 260 |
| [70, 80) | 75 | 2 | 150 |
| 42 | 1 820 |
Medidas de dispersión
Las medidas de dispersión, también llamadas medidas de variabilidad, muestran la variabilidad de una distribución, indicando por medio de un número, si las diferentes puntuaciones de una variable están muy alejadas de la mediana media. Cuanto mayor sea ese valor, mayor será la variabilidad, cuanto menor sea, más homogénea será a la mediana media. Así se sabe si todos los casos son parecidos o varían mucho entre ellos.
Para calcular la variabilidad que una distribución tiene respecto de su media, se calcula la media de las desviaciones de las puntuaciones respecto a la media aritmética. Pero la suma de las desviaciones es siempre cero, así que se adoptan dos clases de estrategias para salvar este problema. Una es tomando las desviaciones en valor absoluto (Desviación media) y otra es tomando las desviaciones al cuadrado (Varianza).
LA VARIANZA (S2 ó δ2 ):
La varianza es una medida de dispersión relativa a algún punto de referencia. Ese punto de referencia es la media aritmética de la distribución. Más específicamente, la varianza es una medida de que tan cerca, o que tan lejos están los diferentes valores de su propia media aritmética. Cuando más lejos están las Xi de su propia media aritmética, mayor es la varianza; cuando más cerca estén las Xi a su media menos es la varianza. Y se define y expresa matemáticamente de la siguiente manera:
La varianza para datos no agrupados
Dado un conjunto de observaciones, tales como X1, X2, … , Xn, la varianza denotada usualmente por la letra minúscula griega δ (sigma) elevada al cuadrado (δ2)y en otros casos S2 según otros analistas, se define como: el cuadrado medio de las desviaciones con respecto a su media aritmética"
Matemáticamente, se expresa como:
Ejemplo:
Se tienen las edades de cinco estudiantes universitarios de Ier año, a saber: 18,23, 25, 27, y 34. Al calcular la media aritmética (promedio de las edades, se obtuvo 25.4 años, encontrar la varianza de las edades de estos estudiantes:
Para calcular se utiliza una tabla estadística de trabajo de la siguiente manera:
Xi
|
( Xi - )
|
( Xi - )2
|
18
|
(18 – 25.5)=-7.4
|
(-7.4)2=54.76
|
23
|
(23 – 25.5)=-2.4
|
(-2.4)2= 5.76
|
25
|
(25 – 25.5)=-0.4
|
(-0.4)2= 0.16
|
27
|
(27 – 25.5)= 1.6
|
( 1.64)2= 2.16
|
34
|
(34 – 25.5)= 8.6
|
( 8.6)2 =73.96
|
Total
|
xxxx
|
137.20
|
Respuesta: la varianza de las edades es de 27.4 años
La varianza para datos agrupados
Si en una tabla de distribución de frecuencias. Los puntos medios de las clases son X1, X2, … , Xn; y las frecuencias de las clases f1, f2, … , fn; la varianza se calcula así:
Σ(Xi-)2f1
δ2 = ----------------
Σfi
Sin embargo la formula anterior tiene algún inconveniente para su uso en la practica, sobre todo cuando se trabaja con números decimales o cuando la media aritmética es un número entero. Asimismo cuando se trabaja con máquinas calculadoras, La tarea de computar la varianza se simplifica utilizando la formula de computación que se da a continuación:
ΣXi2fi - [(ΣXifi)2/N]
δ2 = ----------------------------
N donde N=Σfi
Ejemplo:
Se tienen los datos de una muestra de 30 cuentas por cobrar de la tienda Cabrera’s y Asociados dispuestos en una tabla de distribución de frecuencias, a partir de los cuales se deberá calcular la varianza, para lo cual se construye la siguiente tabla estadística de trabajo, si se calculó anteriormente la media aritmética y se fijó en 43.458 (ver ejemplo del calculo en "media aritmética para datos agrupados) de la siguiente manera
clases
|
Punto medios
Xi
|
fi
|
Xi2
|
Xifi
|
X2fi
|
7.420 – 21.835
|
14.628
|
10
|
213.978
|
146.280
|
2,139.780
|
21.835 – 36.250
|
29.043
|
4
|
843,496
|
116.172
|
3,373.984
|
36.250 – 50.665
|
43.458
|
5
|
1,888.598
|
217.270
|
9,442.990
|
50.665 – 65.080
|
57.873
|
3
|
3,349.284
|
173.619
|
10,047.852
|
65.080 – 79.495
|
72.288
|
3
|
5,225.555
|
216.864
|
15,676.665
|
79.495 – 93.910
|
86.703
|
5
|
7,533.025
|
433.965
|
37,665.125
|
Total
|
XXX
|
30
|
19,053.936
|
1,304.190
|
78,346.396
|
= 21,649.344 / 30 = 721.645
Respuesta: la varianza de las cuentas por cobrar es igual B/.721.645
- Propiedades de la varianza :
- s siempre un valor no negativo, que puede ser igual o distinta de 0. Será 0 solamente cuando Xi=
- La varianza es la medida de dispersión cuadrática optima por ser la menor de todas.
- Si a todos los valores de la variable se le suma una constante la varianza no se modifica. Veámoslo:
Si a xi le sumamos una constante xi’ = xi + k tendremos (sabiendo que 
)
)
- Si todos los valores de la variable se multiplican por una constante la varianza queda multiplicada por el cuadrado de dicha constante. Veámoslo:
Si a xi’ = xi · k tendremos (sabiendo que 
)
)
- Si en una distribución obtenemos una serie de subconjuntos disjuntos, la varianza de la distribución inicial se relaciona con la varianza de cada uno de los subconjuntos mediante la expresión
Siendo
Ni è el nº de elementos del subconjunto (i)
S2i è la varianza del subconjunto (i)
Rango o recorrido
El rango es la diferencia entre el mayor y el menor de los datos de una distribución estadística.
Desviación media
La desviación respecto a la media es la diferencia entre cada valor de la variable estadística y la media aritmética.
Di = x - x
La desviación media es la media aritmética de los valores absolutos de las desviaciones respecto a la media.
La desviación media se representa por 
Ejemplo
Calcular la desviación media de la distribución:
9, 3, 8, 8, 9, 8, 9, 18
Desviación media para datos agrupados
Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la desviación media es:
Ejemplo
Calcular la desviación media de la distribución:
| xi | fi | xi · fi | |x - x| | |x - x| · fi | |
| [10, 15) | 12.5 | 3 | 37.5 | 9.286 | 27.858 |
|---|---|---|---|---|---|
| [15, 20) | 17.5 | 5 | 87.5 | 4.286 | 21.43 |
| [20, 25) | 22.5 | 7 | 157.5 | 0.714 | 4.998 |
| [25, 30) | 27.5 | 4 | 110 | 5.714 | 22.856 |
| [30, 35) | 32.5 | 2 | 65 | 10.174 | 21.428 |
| 21 | 457.5 | 98.57 |
Desviación típica
La desviación típica es la raíz cuadrada de la varianza.
Es decir, la raíz cuadrada de la media de los cuadrados de las puntuaciones de desviación.
La desviación típica se representa por σ.
Desviación típica para datos agrupados
Para simplificar el cálculo vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.
Desviación típica para datos agrupados
Ejercicios de desviación típica
Calcular la desviación típica de la distribución:
9, 3, 8, 8, 9, 8, 9, 18
Calcular la desviación típica de la distribución de la tabla:
| xi | fi | xi · fi | xi2 · fi | |
|---|---|---|---|---|
| [10, 20) | 15 | 1 | 15 | 225 |
| [20, 30) | 25 | 8 | 200 | 5000 |
| [30,40) | 35 | 10 | 350 | 12 250 |
| [40, 50) | 45 | 9 | 405 | 18 225 |
| [50, 60) | 55 | 8 | 440 | 24 200 |
| [60,70) | 65 | 4 | 260 | 16 900 |
| [70, 80) | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |
EMPLEAS LOS CONCEPTOS ELEMENTALES DE LA PROBABILIDAD
PROBABILIDAD CLASICA
PROBABILIDAD CLASICA
Es el número de resultados favorables a la presentación de un evento dividido entre el número total de resultados posibles. Asignación de probabilidad "a priori", si necesidad de realizar el experimento.
La probabilidad clásica o teórica se aplica cuando cada evento simple del espacio muestral tiene la misma probabilidad de ocurrir.
Fórmula para obtener la probabilidad clásica o teórica:
EJEMPLO: ¿Cuál es la probabilidad de obtener un número mayor que 3, en el lanzamiento de un dado? Si E: 4, 5, 6, entonces el número de resultados favorables es n (E) = 3.
Si S: 1, 2, 3, 4, 5, 6, entonces el número total de resultados posibles es (S) = 6.
Por lo tanto:
EJEMPLO: ¿Cuál es la probabilidad de obtener un número mayor que 3, en el lanzamiento de un dado? Si E: 4, 5, 6, entonces el número de resultados favorables es n (E) = 3.
Si S: 1, 2, 3, 4, 5, 6, entonces el número total de resultados posibles es (S) = 6.
Por lo tanto:
FIN
ME SALVO LA VIDA
ResponderEliminar